Keywords: translation, translation initiation, RNA secondary structure, statistical analysis

Effects of the secondary structure of mRNA leader sequences on translation rate are exemplified experimentally. However, no statistical evidence on the role of secondary structure (unlike the average composition effect) at the pre-elongation stage is yet available, since the leader sequences are extremely heterogeneous in both their lengths and nucleotide composition.

We have demonstrated that distribution of relative deviations Z (z-scores) of optimal secondary structure energies of random sequences can be approximated by the normal distribution in most cases, justifying application of standard statistical tests. Two patterns were found while analyzing z-scores of 5’UTRs of plant and mammalian genes with high (H) and low (L) expression levels. In the first (dicot plants) pattern, these regions display relatively uniform composition but deviate considerable from random sequences in stability of their secondary structures. As expected, these deviations of L genes are more pronounced. In the second pattern, typical of mammalian genes, the leader regions are heterogeneous in their average GC composition within each subset and differ from one another even more drastically. However, characteristics of secondary structure of these regions differ insignificantly from the random sequences. The effects observed suggest two possible scenarios of expression regulation. The first scenario involves local functional elements based on secondary structures in the leader regions. The second scenario implies a generalized control of the genes with similar expression levels. Its global order requires a new level of gene organization (for example, their localization in isochores), what supports a selection hypothesis of compositional transition in higher organisms.

Recent success in sequencing provided bioinformatics with a possibility to analyze unexampled data massifs. The tremendous volume of sequences obtained allows weak dependencies, insignificant in case of small-volume samples, to be revealed. As a rule, the sequences analyzed are heterogeneous (according to definition [1], as they are composed of statistically distinct subgroups due to evolutionary dependence, spotty sequencing, dependencies of control indicators on processing algorithms and inessential parameters of sequences, etc.), impeding obtaining reliable conclusions.

This work describes the computer analysis of secondary structures of mRNA leader regions using a program based on genetic algorithm (GA). The algorithm speed [2] allows mass calculations of secondary structures to be performed. The energy of secondary structure in parameterization of Turner et al. [3] is employed as a control indicator. The difficulties encountered while analyzing are of general character, in particular, they are independent of the function optimized. Let us consider two difficulties in detail:

1. GA does not guarantee the optimal solution. In addition, the optimization itself depends not only on the algorithm settings, but also on parameters of a sequence, in particular, its length and nucleotide composition.
2. More important is the fact that the energy of the secondary structure itself depends on the same parameters.

Therefore, it is actually difficult to form a uniform set of data (where the distinctions between the sequences are limited by the effects of factors inessential for the analysis and may, thus, be considered as random).

Typical of the structural properties of RNAs and proteins is a strong dependence even on the average alphabetical content, whereas the diversity of structures and functions is determined by the order of symbols. Thus, it is expedient in mass analysis to compare naturally occurring sequences with the sequences displaying similar average compositions and random order of symbols (the "null hypothesis"). Since the distributions of control indicators are unknown a priori, the technique of relative deviations (z-scores) is frequently used. Lattice proteins, conventional proteins and their structures generated by threading, and RNAs divided into small subsequences were the objects of such analysis. Typical of sequences in these examples are equal lengths, which is unusual for natural data. In addition, the conclusions made are qualitative and not statistically substantiated.

The program Fitness [2] based on the GA was used in this work. The release used has the following additions compared with the previous release described in detail in [2]: (a) the secondary structures considered now contain no thermodynamically unfavorable helices and (b) inhibition of stems composed by partially overlapping stems (the so-called running loops [4]) is canceled.

As a result of (a), the algorithm finds the optimal or close to optimal structure of sequences up to 300 nt long (Fig. 1). In the previous release, the "high frequency" noise on the surface of free energy trapped the sequences longer than 150- 200 nt in the local optima.

Although addition (b) fails to provide an essential improvement of the optimum reached, it is very important for the accuracy of the structure prediction. Our calculations using random sequences have demonstrated that the fraction of running loops increases with sequence length (Table 1), as one would expect. Due to (b), the search space for the algorithm increases considerably, but the calculation time does not. Depending on the alphabet, the optimization speed is ordered as GC<AU<AUGC, complying with a smoother landscape of the free energy for alphabets with a higher size and lower energy of complementary bonds [5].

Relative deviation (or z-score) of a random variable x is determined as

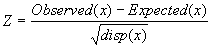Our calculations (Fig. 1) suggest that distributions of the free energy z-scores of random sequences not exceeding 300 nucleotides are statistically uniform with respect to the length and compositions of these sequences. It is evident that the z-score distribution itself belongs to the class of limit distributions and important that it can be approximated by the normal distribution in most cases (Table 1). Thus, we may use standard statistical procedures for testing the hypotheses on higher or lower stability of the secondary structures of the sequences under study compared to the random sequences of the same lengths and compositions. Essentially, heterogeneity of the sample studied with respect to these parameters is allowed.

Statistical analysis described above addresses the question to what extent the secondary structure of natural RNAs is important. Genes displaying high and low expression levels (selection of sequences is detailed in the work of Vorobiev et al., this issue) are most convenient objects for such a study, as they allow the analysis to be reduced to comparison.

The samples of H and L genes appeared to be considerably heterogeneous in both their primary and secondary structures (Table 2). However, two patterns may be separated. In the first (mammals), H and L genes differ considerably in their average compositions: L genes display an essentially higher fraction of GC nucleotides (compare the structure energies of 50% and 100% GC sequences in Table 1). In addition, the deviations of secondary structure stabilities of H and L genes are opposite (insignificantly, from the random sequences; significantly, from one another).

In the second pattern (dicot plants), the sequences are essentially more uniform in their composition both between and within the H and L sets. Compared with the mammalian genes, they are GC-poor and display smaller GC variations despite the greater sample volume. A weak effect of z-scores of secondary structure stability is, in contrary, significant. The pooled sample of H and L genes follows the same pattern.

The hypothesis on translation efficiency is most popular (compared with transcription maximization and mutation bias hypotheses) while interpreting the usage of synonymous codons in different genomes. Higher rates of both translation and transcription may result in a higher level of gene expression. Optimization of the rates of successive (stationary) processes (for instance, translation initiation and elongation of peptide chain) through selection would lead to their coordination with respect to efficiency. The easiest way to reach this is to control the factors common for all the processes. On the one hand, their rates should be coordinated, as long as the yield of peptide chain is a limiting factor. On the other, these processes are not akin, including the mRNA regions involved. This leads to differences in the corresponding regulatory mechanisms. Rare codons within the coding region slow down the ribosome movement, as does secondary structure within leader region [6].

The energy of RNA secondary structure depends mainly on the average nucleotide composition (Table 1), as confirmed through processing a great number of random sequences [5]. The difference between the structural characteristics of coding regions of high- and low-expression genes in one of the first observations [7] and further application of only context analysis of leader regions [8] is connected with the domination of this effect. (Individual regions of a pre-mRNA differ insignificantly in their nucleotide content [9].) The technique of z-scores allows the effect of the secondary structure to be separated from the trivial consequence of average composition, e.g. environmental temperature.

Our observations suggest two possible scenarios of expression regulation — local and global. The local scenario is observed in plants and connected with differential modulation of leader regions by secondary structure elements, playing the role of conventional functional elements. The global scenario is typical of higher organisms and based on generalized control of the genes with similar expression levels through close localization in isochores. A compositional transition to warm-blooded isochore structure [10] may have made an emergence of such a "blockwise" regulatory mechanism easier.

We are grateful to G. Chirikova for translating this manuscript to English. The work was supported by the INTAS-RFBR grant 95-0653.

1. Feller W. An introduction to probability theory and its applications. John Wiley & Sons, 1970.
2. Titov I.I., Ivanisenko V.A., Kolchanov N.A. (2000) Comp. Tech. 5 (in press).
3. Turner D.H., Sugimoto N., Freier S.M. (1988) Annu. Rev. Biophys. Biophys. Chem. 17, 167.
4. Studnicka G.M., Rahu J.M., Cummings I.M., Salser W.A. (1978) NAR 5, 3365.
5. Fontana W., Konnings D.A.M., Stadler P.F., Schuster P. (1993) Biopolymers 33, 1389.
6. Kozak M. (1994) Biochimie 76, 815.
7. Ischenko I.V., Kel A.E., Omelyanchuk L.V., Kolchanov N.A. (1993) In: Computer analisis of genetic macromolecules. Structure, function and evolution. (World Scientific Publishing; Eds: H. Lim and N.A. Kolchanov), pp.156-167.
8. Kochetov A.V., Ischenko I.V., Vorobiev D.G., Kel A.E., Babenko V.N., Kisselev L.L., Kolchanov N.A. (1998) FEBS Lett. 440, 351.
9. Clay O., Cacciò S., Zoubak S., Mouchiroud D., Bernardi G. (1996) Mol. Phylogenet. Evol. 5, 2.
10. Bernardi G., Bernardi G. (1986) J. Mol. Evol. 24, 1.