Utility of applying the features for site activity prediction
A deviation D n=Fzmw(Sn)-Fn of predicted activity value from the experimental one is calculated. For the values {Fzmw(Sn), Fn, D n}, 11 conditions of regression analysis were tested (Forster and Ronr, 1979). In order to minimize the influence of heterogeneity of the tested values {Fzmw(Sn), Fn, D n}, this set is subdivided into two non-overlapping subsets equal in volume. The testing of all 11 conditions is made independently for each of two subsets. Besides, by the corresponding statistical criterion, the level of significance a rt, is estimated, so that the r-th condition (1£ r£ 11) holds for the t-th subset (1£ t£ 2). Since these checked requirements are of different essence, the Fuzzy logic (Zadeh, 1965) is applied to generalise each criterion-specific a rt for the tested feature XZmw to the universal scale urt(Xzmw, F), the so-called "utility", which is estimated as:
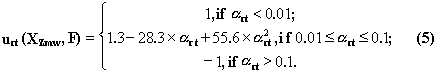
According to the utility theory for decision making (Fishburn, 1970), urt(Xzmw, F) is called "partial utility of applying the features XZmw for predicting the activity F". After testing all 11 conditions for two subsets, the feature XZmw is provided by 11´ 2=22 partial utilities urt(Xzmw, F). Their mean value represents "the integral utility of the feature XZmw for predicting the activity F" (Fishburn, 1970):