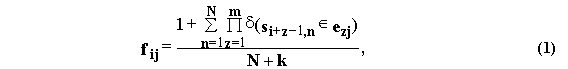
Oligonucleotide frequency matrix
For a oligonucleotide frequency matrix construction, the site set {S1...Sn...SN } was used.
It contains N nucleotide sequences Sn=s1n...sin...sLn of L bp in length determined experimentally (where, sÎ {A, T, G, C}). All these sequences are multiply aligned by the standard Gibbs-potential method (Lawrence, 1994).
The oligonucleotide alphabet {E1, ..., Ej, ..., Ek} of k pseudoletters Ej={e1je2j...emj} of m bp in length is fixed (where, eÎ {A, T, G, C, W=(A, T), S=(G, C), R=(A, G), Y=(T, C), M=(A, C), K=(T, G)}). In these definitions, the oligonucleotide frequency matrix FL-m+1,k={fij} is calculated as follows:
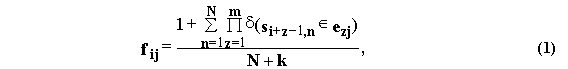
where d(true)=1, d(false)=0.
Formula (1) estimates the frequency value fij of the pseudoletter Ej occupying the i-th position within the site sequences multiply aligned, in case the total number of these sequences N is much more than the total number of pseudoletters k in the oligonucleotide alphabets used. That is why, in this work, formula (1) was applied to the alphabets #1, #6, #7, #9, #13, #14, #17, #20, #21, #25, when N>8; to the alphabets #10, #15, #22, when N>25; to the alphabets #2, #4, #16, #26, when N>65; and, finally, to the alphabet #5, when N>200.