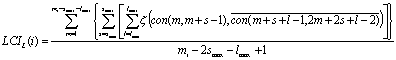EEI-Calculator

Summary

Introduction

Methods and Algorithms

Genome sequences

Local complementarity index (LCI)

Elongation Efficiency Index (EEI)

5 forms of EEI

Estimation of correlation between EEI and gene expression

Output

Examples

Acknowledgements

Contacts

References

Summary

We developed an algorithm for estimating general translational characteristics of an organism using its genome sequence. The algorithm computes elongation efficiency index (EEI) in five different forms for each ORF. Computation is based on estimation of ORF elongation efficiency considering three key factors: codon bias, average number of inverted repeats within coding sequence, and free energy of potential stem-loop structures. The impacts of these factors on translation are numerically estimated.

EEI-Calculator allows to estimate whether gene expression in given organism is correlated with selection towards preferred codons (high M₁) and/or selection against secondary structures (high M₂,..M₅). This knowledge may be useful in planning transgenic studies with recently sequenced unicellular organisms.

Introduction

Elongation is the most energy- and time-consuming stage of mRNA translation. Therefore, high level of gene expression requires high rate of elongation. In many unicellular organisms this is achieved by non-uniform usage of synonymous codons, with preferences for a subset of “optimal” codons in highly-expressed genes (Sharp and Li, 1987; Andersson and Kurland, 1990). The sets of preferred codons in such organisms have high relative concentrations of cognate tRNAs (Ikemura1985; Gouy and Gautier, 1982). Codon bias increases translation rate because preferred codons tend to be translated more rapidly than synonymous alternatives (Sorensen 1989; Kurland 1991). Translational codon bias is correlated with gene expression level in many prokaryotes and some eukaryotes (Ikemura 1985; Gouy and Gautier, 1982; Duret and Mouchiroud, 1999).

Though codon bias indices like CAI (Sharp and Li, 1987) are good predictors of gene expression in E. coli, B. subtilis and many other organisms, they are not useful for organisms which do not have strong translational codon bias. This set of species includes Helicobacter pylori (Lafay et al., 2000), Borrelia burgdorferi (Lafay et al., 1999) and others. In these species codon bias is not correlated with gene expression, and indices like CAI can not be applied to gene expression prediction.

This problem prompted the authors to consider the negative influence of RNA secondary structures on the rate of elongation (Likhoshvai and Matushkin, 2002). To estimate this influence, authors proposed to calculate the average number of local inverted complementary repeats within ORF, which may form local stem-loop structures.

Indeed, this approach revealed correlation between gene expression and translational index in those organisms where traditional codon bias indices like CAI do not work. The constructed elongation efficiency index (EEI) has five forms according to the included key factors:

1. codon composition
2. number and length of local hairpins
3. number, length and energy of local hairpins
4. codon composition + number and length of hairpins
5. codon composition + number, length and energy of hairpins

According to their leading EEI forms, organisms were classified by five translational groups (Likhoshvai and Matushkin, 2002).

Methods and Algorithms

Genome sequences

The flat file(s) of complete genome sequence in Genbank or EMBL format are uploaded by the user. The sequenced genomes may be found in NCBI GenBank FTP or EMBL. From each file coding sequences of genes longer than 30 codons, with 3’- and 5’-flanking regions of 600 nucleotides, are extracted.

Local complementarity index (LCI)

In order to estimate influence of local secondary structures on elongation efficiency, authors proposed a local complementarity index (LCI) in two forms.

In the first form (LCI_L) the average number of self-complementary regions in a window of m_i nucleotides is calculated according to the following formula:

In this computation we disregard information about the energy of hairpins formed in mRNA. In the latter formula con(i,j) is the sequence of nucleotides between the i-th and j-th nucleotides, and - denotes sequence that is complementary to nucleotide sequence the j-th and i-th nucleotides (i £ j); and z(context1,context2) has value 1, if the words context1 and context2 are identical, otherwise z(context1,context2)=0; i=1,..N_tot, where N_tot is the total number of extracted ORFs from the genome. The length of accountable inverted repeat falls between s_min and s_max; the distance between accountable inverted repeats falls between l_min and l_max (in this paper, we accept s_min=s_max=3, l_min=12, l_max=85).

The LCI_L(i) value has a meaning of the number of complementary nucleotides per one nucleotide in ORF_i.

In the second form (LCI_E) the average free energy of hairpin formed in the window of m_i nucleotides is calculated with the following formula:

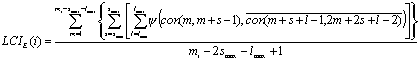
where y is an energy of the secondary structure, which is calculated conventionally (Turner and Sugimoto, 1988).

The LCI_E(i) value has a meaning of average free energy of complementary secondary structures per one nucleotide.

Elongation Efficiency Index (EEI)

After calculation of LCI_L(i) and LCI_E(i) indices for each ORF_i, an iterative algorithm ranks ORFs according to their EEI values (with all five EEI types). At the first step, a random sample of N_sub=150 ORFs is chosen, and frequencies of all codons are counted in it. According to the obtained codon frequencies, the EEI values are calculated for all ORFs. The EEI(i) value reflects the relative average elongation rate of one codon in the ORF_i:

EEI(i)=K/(w₁T_a(i)+w₂T_e(i)), where K is a scale constant, w₁=(0 or 1), and w₂=(0 or 1) are weight coefficients.

The first term T_a evaluates the codon bias. It reflects the mean time required for fixation of isoacceptor aminoacyl-tRNA in the А-site of a ribosome as determined by codon frequencies alone:

,

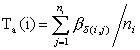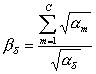, where the variable 1/b_d(i,j) is interpreted as the optimal relative concentration of cognate tRNA for the j-th accountable codon, while a_d is a frequency of d codon in reference sample of genes, and n_i is the number of codons in ORF_i.

The second term, T_e(i), estimates the mean time required for translocation:

T_e(i)= t_min (1-p(i))+t_max p(i),

where t_min is a minimal, t_max is the maximal conventional times required for translocation, p(i) is the probability of realization of the maximal conventional time calculated by the following equation:

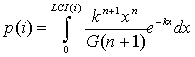, k=m/s², n=(m/s)², where m is the mean and s² is the dispersion of positive random variable with distribution density of , and G(n+1) is Gamma-function.

After calculation of EEI(i) (i=1,…,N_tot), all ORFs are ranked by EEI values, and next sample of N_sub ORFs with the highest EEI values is chosen. This procedure is cyclically repeated until the set of ORFs comprising the reference sample becomes constant. Usually it takes 10-15 iterations.

The number N_sub=150 sample ORFs was used from considerations of virtually constant number of house-keeping genes in unicellular organisms.

When the iterative algorithm is completed, all ORFs are again ranked by EEI values.

5 forms of EEI

Weight coefficients w₁, w₂ have values 0 or 1, and LCI(i) may be of two types, LCI_L(i) or LCI_E(i), so there are 5 forms of EEI:

1) EEI₁ (A), w₁=1, w₂=0, no LCI. Only codon bias is considered, and secondary structures are neglected.

2) EEI₂ (LCI_L), w₁=0, w₂=1, LCI(i)=LCI_L(i). Codon bias is neglected. Only number and length of secondary structures are considered.

3) EEI₃ (LCI_E), w₁=0, w₂=1, LCI(i)=LCI_E(i). Codon bias is neglected. Only number and free energy of secondary structures are considered.

4) EEI₄ (A-LCI_L), w₁=1, w₂=1, LCI(i)=LCI_L(i). Both codon bias and number of secondary structures with account of their length are considered.

5) EEI₅ (A-LCI_E), w₁=1, w₂=1, LCI(i)=LCI_E(i). Both codon bias and number of secondary structures with account of their energy are considered.

Estimation of correlation between EEI and gene expression

To estimate correlation of EEI with gene expression levels we used the well known fact that ribosomal genes are normally highly-expressed in unicellular organisms. Hence, they may be used as markers to evaluate the ability of EEI to predict gene expression.

In each genome we marked genes involved in ribosomal subunits formation. This procedure is performed automatically by Perl-script, which recognizes and marks up the ribosomal genes using combinations of key words in gene annotation.

For each of five index types a pair of (M±R) is calculated, where M is the mean of positions of ribosomal genes among all genes ranked by EEI, and R is the standard deviation of positions:

,

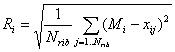
The (M±R) pair has a meaning of relative elongation efficiency of ribosomal genes.

As a result, we obtain five pairs of (M₁±R₁), (M₂±R₂), (M₃±R₃), (M₄±R₄), (M₅±R₅), which reflect the translational characteristics of the organism. Hereinafter pairs (M_i±R_i) are normalized within the limits of (-100<M<100) and (0<R<100) for convenience.

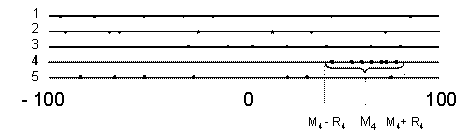
In Fig. 1 one can see a typical distribution of relative EEI_i values of ribosomal genes. High relative elongation efficiency of ribosomal genes is observed here in EEI₄. The criterion of high correlation between EEI_i and gene expression is the closeness of M_i to +100 (and, in addition, low R_i). High M_i indicates that ribosomal genes have relatively high expression levels among other genes, and low R_i indicates that their expression is tightly correlated with each other.

Figure 1. Scheme of relative elongation efficiency distributions for ribosomal genes. Genes are ranked by EEI_i, i=1,…,5. High relative elongation efficiency is observed in EEI₄.

The statistical significance of M_i±R_i realization was estimated using Monte Carlo simulations. The null hypothesis consisted in random distribution of relative elongation efficiencies of ribosomal genes.

Even in organisms with small total number of genes, the significance of M_i is very high despite the small sample size. For example, in Candidatus Blochmannia floridanus, with N_rib=54, N_tot=584, the mean M₄=36 and standard deviation R₄=53, the significance is p=10^-6. For most genomes the statistical significance is even higher (p@10^-8-10^-12).

During the EEI_i calculation we excluded short 5’- and 3’-regions of ORFs, because their codon composition may be biased due to initiation and termination effects. The length of excluded regions varied from 1 to 20 codons, and was determined by an algorithm of seeking the maximal M₁ value.

Output

The program output contains the following results:

General genome statistics

N_rib, number of recognized ribosomal genes

N_tot, total number of considered ORFs

L, length of the genome (Kbp)

G+C composition (%)

Translational characteristics

M₁±R₁ (codon composition)

M₂±R₂ (number and length of local hairpins)

M₃±R₃ (number and energy of local hairpins)

M₄±R₄ (codon composition + number and length of l. h.)

M₅±R₅ (codon composition + number and energy of l. h.)

G, the translational group (number of the largest index M with smallest R)

If the organism falls into group 1, its gene expression is correlated with selection towards preferred codons (high M1). In practice this means that replacing of suboptimal codons by preferred synonymous codons may increase transgene expression in the given host organism. The well known examples of such organisms are Escherichia coli and Bacillus subtilis.

Organisms that fall into groups 2 and 3 (low M₁ and high M₂, M₃) have no strong correlation between gene expression and codon composition. In such organisms replacing of codons will unlikely result in higher gene expression. Instead, stable secondary structures should be minimized along ORF to enhance its expression.

Those organisms that fall into groups 4 and 5 (high M₄ and M₅) have both preferences in codon usage and selection against secondary structures. In transgenic design both these factors should be taken into account for increasing gene expression.

Examples

The values of the (M_i,R_i) pairs for some bacteria are shown in Table 1. The cumulative diagram of bacterial genome distribution over five translational groups is shown in Fig. 2. Most bacterial genomes fall into Groups 1 and 4.

Table 1. Relative elongation efficiency of ribosomal genes in some bacterial genomes.

Genome	Num of ribos. genes	Num of all genes	M1±R1	M2±R2	M3±R3	M4±R4	M5±R5	Group
Escherichia coli K12	56	4234	92±23	25±64	28±57	79±37	65±53	1
Mycoplasma hyopneumoniae 232	48	691	-56±55	73±34	64±44	41±53	47±51	2
Nitrosomonas europaea	55	2573	-52±60	18±67	63±47	-6±69	57±49	3
Borrelia burgdorferi	53	848	-14±60	57±47	57±52	65±41	53±50	4
Pseudomonas putida KT2440	54	5350	74±26	60±33	67±27	86±17	92±13	5

-100<M_i<100, 0<R_i<100 (i=1,..,5) are normalized mean and standard deviations of ribosomal genes positions among other genes ranked by EEI_i values. The highest M_i with corresponding R_i (i=1,..,5) are highlighted.

Using the algorithm we have computed quantitative translational characteristics of 240 unicellular organisms (213 bacteria, 22 archaea, and 5 eukaryota). According to their leading group number, all studied organisms may be classified by five translational groups (see Fig. 2 for Bacteria and Archaea distributions).

Figure 2. Distribution of 213 bacterial and 22 archaeal genomes over five translational groups.

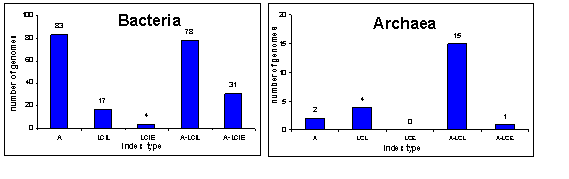
Legend: A – group with preferences in codon usage, LCIL – secondary structures with account of length, LCIE - secondary structures with account of energy, A-LCIL – codon usage with secondary structures with respect to length, A-LCIE – codon usage with secondary structures with respect to energy.

Acknowledgements

The work was supported by the Russian Foundation for Basic Research (No 04-01-00458, 05-04-49068, 05-07-90274, 06-04-49556), Russian Ministry of Industry, Science and Technology (No.43.073.1.1.1501), Siberian Branch of the Russian Academy of Science (project № 10.4), Integration Project № 119, and State contract № 10104-71/П-25/155-270/200605-056 and NSF:FIBR (Grant EF–0330786).

Contacts

Authors: N. V. Vladimirov, V. A. Likhoshvai , Yu. G. Matushkin

Web-version: M.A. Genaev

Institute of Cytology and Genetics SB RAS, Novosibirsk, Russia

References

1. Andersson SGE, Kurland CG (1990) Codon preferences in free-living microorganisms. Microbiol. Rev., 54: 198-210.

2. Carbone A, Zinovyev A, Kepes F (2003) Codon adaptation index as a measure of dominating codon bias. Bioinformatics, 19(16):2005-15.

3. Duret L, Mouchiroud D (1999) Expression pattern and, surprisingly, gene length shape codon usage in Caenorhabditis, Drosophila, and Arabidopsis. Proc. Natl Acad. Sci. USA, 96(8):4482–4487.

4. Gouy M, Gautier Ch (1982) Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res., 10:7055–7070.

5. Ikemura T (1985) Codon usage and tRNA content in unicellular and multicellular organisms. Mol. Biol. Evol., 2:13–34.

6. Kurland CG (1991) Codon bias and gene expression. FEBS Lett., 285(2):165-9.

7. Lafay B, Atherton JC, Sharp PM (2000) Absence of translationally selected synonymous codon usage bias in Helicobacter pylori. Microbiology, 146:851–860.

8. Lafay B, Lloyd AT, McLean MJ, Devine KM, Sharp PM, Wolfe KH (1999) Proteome composition and codon usage in spirochaetes: species-specific and DNA strand-specific mutational biases. Nucleic Acids Res., 27:1642–1649.

9. Likhoshvai VA, Matushkin YG (2002) Differentiation of single-cell organisms according to elongation stages crucial for gene expression efficacy. FEBS Letters, 516:87-92.

10. Sharp PM, Li WH (1987) The codon adaptation index - a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acid Res., 15:1281–1295.

11. Sorensen MA, Kurland CG, Pedersen S (1989) Codon usage determines translation rate in Escherichia coli. J. Mol. Biol., 207:365-377.

12. Turner DH, Sugimoto N (1988) RNA structure prediction. Annu Rev Biophys Biophys Chem., 17:167-92.

Return to EEI-Calculator