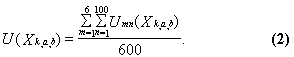
Utility
The difference between the distributions Xk,a,b{S} and Xk,a,b{R} of conformational or physico-chemical features is tested for significance using four statistical criteria (Lehman, 1959): (1) the difference between the means of Xk,a,b{S} and Xk,a,b{R}; (2) the difference between the variances of Xk,a,b{S} and Xk,a,b{R}; (3) the difference between the densities of Xk,a,b{S} and Xk,a,b{R}; and (4) the difference between the ranges of Xk,a,b{S} and Xk,a,b{R}. As the criteria used imply that the tested distributions were Gaussian, two additional criteria were used to confirm it: (5) for Xk,a,b{S} and (6) for Xk,a,b{R}. To reduce the adverse effects of heterogeneity, these criteria were tested on 100 subsets {Sn} and {Rn} (1£ n£ 100), each randomly retrieved from {S} and {R}, respectively. In terms of fuzzy logic (Zadeh, 1965), if the difference between the distributions Xk,a,b{Sn} and Xk,a,b{Rn} is significant according to the m-th criterion (1£ m£ 6), then a positive between 0 and 1 is assigned to the partial utility Umn(Xk,a,b); otherwise, a negative between -1 and 0. Hence, the total number of partial utilities is 6´ 100=600 {Umn(Xk,a,b)}. In terms of decision making theory (Fishburn, 1970), the generalised difference between Xk,a,b{S} and Xk,a,b{R} is the mean of the 600 partial utilities:
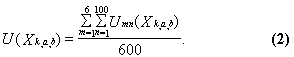
Thus calculated utility value U(Xk,a,b) is the integral characteristic of the discriminating ability of Xk,a,b. It has two important features (Fishburn, 1970):
|
U(Xk,a,b)<0 |
implies that “Xk,a,b falls short of significance”; |
(3) |
|
U(Xk,a,b)>U(Xq,c,d)³ 0 |
implies that “Xk,a,b is better discriminating Site/Random than Xq,c,d” |
(4) |
Note that the highest value of U(Xk,a,b) pinpoints to the best, in terms of utility, B-DNA feature Xk,a,b of the site. Each conformational feature Xk,a,b with U(Xk,a,b)<0 is discarded by decision (3). If any two features Xk,a,b and Xq,c,d correlate, the feature Xq,c,d with the lowest value of U(Xq,c,d) is discarded by decision (4).