This page contains description of of parameters of the input page.
Access to the program: LZcomposer
List of biological tasks that could be solved by using the program for estimation complexity based on Lempel-Ziv algotithm:
Review of other methods of complexity analysis
Data input:
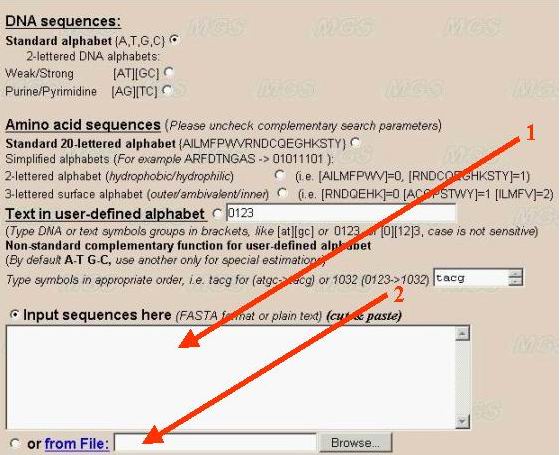
The sequence to be analyzed should be entered into the text-box in the FASTA-format (arrow number 1). The divisor between separate sequences is the line with the first symbol '>'. The sequence can be entered from file of the user's computer by clicking the option 'From file' (number 2).

If there is only a single sequence to be analyzed, you may input this sequence in a plain text format without the comment line. The program has limitations a sequence length 240 Mb (up to size of largest human chromosome). For large sequences please use 'from File' download.
It is recommended to make complexity decomposition for sequence not longer 5-10 Mb due to operating memory restriction. Longer sequences (>12 Mb) could be analyzed by profile method (sliding window) only. size of sliding window is up to 10 Mb.
Program options:
Let us determine the alphabet. It is recommended to use the default alphabet
(A, T, G and C; number 1 in the figure) for DNA sequence analysis.
It is possible to use another combinations (for example, A/T, G/C} for studying
GC-content in binary alphabet (number 2 and 3).
A user may use another combination of letters by choosing the option 'User
defined alphabet'. Then a user may set in a text-box the alphabet (number
7), for example, in a form [AT][GC] or [TC][AG], or A[CGT]. The symbols in
square brackets are interpreted as a single symbol. The symbols that are
not indicated in alphabet will be ignored.
Predefined DNA alphabets: Weak-Strong DNA alphabet: W=A/T, S=G/C; Purine-Pyrimidine DNA alphabet: R=A/G, Y=T/C; Amino-Keto DNA alphabet: M=A/C, Y=G/T.
A DNA sequence will be converted to user-selected alphabet automatically without any prompt. Program uses digital presentation of symbols for calculation (0,1,2,...) and alphabet is important only for data presentation.
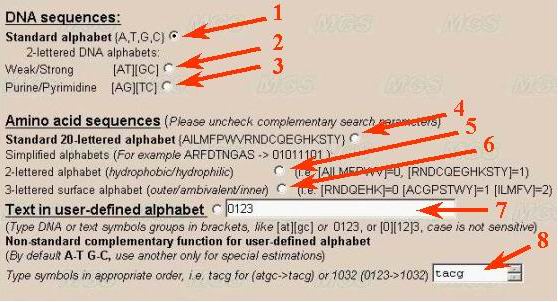
To analyze amino acid sequences, choose the alphabet for analysis of the
protein sequence (ACDEFGHIKLMNPQRSTVWY). In this case, the parameters of nucleotide alphabet are
ignored.
We suggest the following variants of grouping amino acid residues:
by hydrophobicity-hydrophilicity, i.e. [AILMFPWV] - hydrophobic and [RNDCQEGHKSTY] - hydrophilic (number 4 in the figure)
by charge (number 5 in the figure), [RHK] - basic, [ANCQGILMFPSTWYV] - neutral, [DE] - acidic
by surface location (inner location in protein globule or surface location) [RNDQEHK] - outer, [ACGPSTWY] - ambivalent, and [ILMFV] - inner.
A user may order his own variant of partitioning by ordering in appropriate window the line indicating how to group the symbols (number 7). By ordering by a user of his own alphabet, the residues that are not indicated will be ignored.
User can define own complementarity function
(number 8). It means that each letter in user-defined alphabet will have correspondent
letter to be used in the compression algorithm. For example, standard complementarity
order for {A,T,G,C} could be presented as {T,A,C,G}. The order of letters
is important.
It is not recommended to use complementary search parameters for non-DNA alphabet.
Only a single type of the alphabet should be chosen (see numbers 1-7).
The program parameters of calculation method are ordered as indicated by arrows in the figure below:
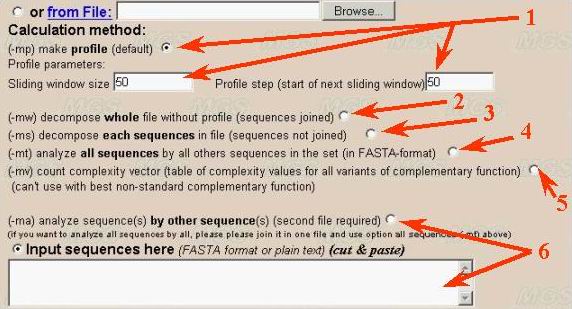
(1) User should select the calculation method for complexity decomposition. First variant is calculation of complexity profile of a sequence by sliding window (number 1). Default sliding window size is 50 nt. Step of profile equals 50 nt by default. As the result user will obtain an array of digits (currently in text format).
(2) The second variant (number 2 in the figure) is decomposition of the whole sequence (or joined sequences in the sample). The result will be presented as set of non-overlapped sequence fragment with supplementary information about localization and repeat types. The resulting decomposition output is large text (approximately four times greater than the sequence under analysis).
(3) The third variant presents full complexity decomposition of a set of sequences in FASTA-format (number 3).
(4) The fourth variant corresponds to complexity decomposition of all sequences
in the set by other sequences (number 4). It means that repeat prototypes
are taken from another sequences, but not from the sequence itself as for
the methods described above. The result is table of mutual relatedness of
sequences in the set measured as edition distance corresponding to complexity
decomposition in this case.
(5) The fifth variant of calculation presents complexity decomposition based on all theoretically possible variants of correspondence (complementarity) function (number 5). This method of complexity analysis could be used for comparison of different variants of data compression.
(6) Analysis of one sequence by another one demands second sequence input
in separate window (number 6). This variant of complexity decomposition ids
intended for analysis of evolutionary relationship between sequences. Two
different sets of sequences in FASTA-format could be used also for such decomposition
of first set by the second.
In later case user should use both two input windows for first (number 1) and second (number 2) sequences in the program interface (see below). Both "cut and paste" and file downloading inputs are available. The second input window is not need for complexity profile calculation, whole sequence decomposition and its variants (methods 1-5 described above).
Repeat types, output parameters and program execution
User can select any possible combinations of four repeat types for complexity
decomposition (number 1). But at least one repeats type should be selected.
Classification of repeats in DNA sequences (short examples):
1) Direct (type D) AGCTTA...AGCTTA
2) Symmetric (type S) AGCTTA...ATTCGA
3) Inverted (symmetric complementary) (type I) AGCTTA...TAACGT
4) Direct Complementary (type C) AGCTTA...TCGAAT
It is recommended to use direct and inverted repeats due to their biological
significance.
Calculation based on automatic choice of correspondence (complementarity)
function is also available (number 2). All selected repeat types will be ignored
in this case.
Parameters for the program output are indicated by numbers 3-7 in the figure.
User can select minimal output (number 3). It means only complexity value
(integer number, minimal number of non-overlapped fragments). Full detailed
text output of all fragments in decomposition is also available (number 4).
It is not recommended use full detailed report for longer sequences (longer
than 1Mb, like complete microbial genomes). Other variants (number 5-7) correspond
to restricted text output and statistic of repeat distribution (for whole
text decomposition only). Statistical parameters include distribution of long
repeats in decomposition, types and distance between such repeats and so on.
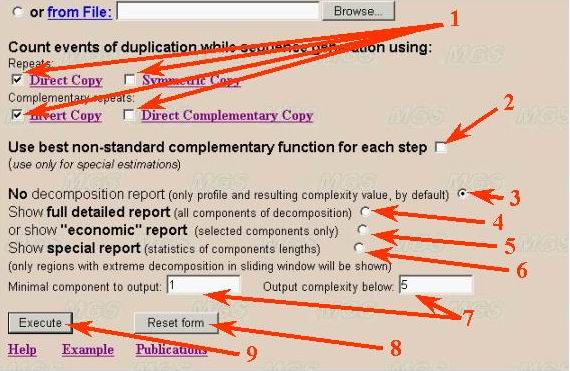
Button "Reset form" allows to reset all checked parameters to default values
(number 8).
The program is executed by clicking the button 'Execute' (see number 9 in
figure given above).
Data output:
The program outputs the results in a textual format. (Position and complexity value in corresponding sliding window).
Short example of the
data output (complexity profile for window 20 bp) looks like column of digits:
0 13 1 12 2 13 3 12 4 12 5 13 6 12 7 12 8 11
...
Another example (whole file decomposition, full detailed report) presents
step by step all fragments of complexity decomposition of the sequence
(promoter).
The output looks like:
Compose whole file:
1 ([1:1],1,NW,'a')
2 ([1:1],1,I<,'t')
3 ([1:1],1,NW,'g')
4 ([1:3],1,D>,'g')
5 ([1:2],1,I<,'a')
6 ([1:3],1,D>,'g')
7 ([1:3],3,I<,'tcc')
10 ([1:2],1,D>,'t')
11 ([1:2],2,D>,'tg')
13 ([1:4],3,I<,'ctc')
...
References to algorithm description:
and implementations: promoter
complexity, complete
bacterial genomes complexity comparison
Comments and questions are welcome to Yu.Orlov.