Method overview
The essence of our approach was as follows. A set of N aligned
(phased) DNA sequences with the length L (without gaps) is considered. A
value of a certain physicochemical or conformational property F
i is ascribed to each dinucleotide. Consequently, the
matrix with a size N*(L - 1) is formed. An element of
this matrix Fikl corresponds to the value of this
particular property Fi of dinucleotide at the
kth position in the sequence l.
The mean value of the property
i at position l amounts to
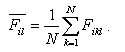 (1) (1)
Variance
is used as a measure of conservation of the ith property for each position
l :
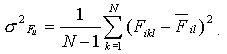 (2) (2)
It is assumed that if a particular property
Fil at particular location l within the nucleotide
sequence is important for the function of the binding site, the value of
this property is conserved for all the sequences of the set, providing a
low value of the variance compared with a set of random sequences. Thus, a
low variance of a particular property indicates its conservation at a
particular position l. The significance of 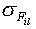 is
estimated using is
estimated using 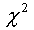 test (Anderson, 1958). test (Anderson, 1958).
Then, we are
assuming that the probability Pil of the ith
property at position l of the sequence analyzed to take the value
Fil required for the function at the value follows a
Gaussian distribution:
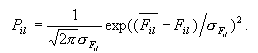 (3) (3)
Let us
select a sum of all the significantly conservative properties normalized
to the number of these properties as a measure of similarity between the
sequences of the set and the sequence analyzed.
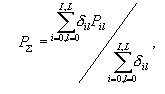 ,
(4) ,
(4)
where 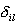 = 1, if = 1, if 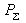 is
significantly low, otherwise = 0.The value corresponds to the probability
of the properties of the DNA sequence analyzed to be close to the detected
conservative properties of the sequences forming the initial set. Let us
designate this value as the level of required conformational similarity
or, in other words, this value is considered to be a "score" value and is
compared with the particular "threshold" value to decide whether this
sequence could be a "site" or "not site". is
significantly low, otherwise = 0.The value corresponds to the probability
of the properties of the DNA sequence analyzed to be close to the detected
conservative properties of the sequences forming the initial set. Let us
designate this value as the level of required conformational similarity
or, in other words, this value is considered to be a "score" value and is
compared with the particular "threshold" value to decide whether this
sequence could be a "site" or "not site".
In addition, in this program we
realized two algorithms for selection for selection of characteristics
that would be most informative for recognition. In this case, basing on
the data on mutual correlation of properties, weights Wil
are ascribed to each probability Pil, so that the weight
of the most informative characteristics is maximized. This allows us to remove
the noise added by less informative characteristics during recognition.
REFERENCES
1. Anderson, T.W. (1958) An Introduction to
Multivariate Statistical Analysis. John Wiley & Sons Inc. NY
|

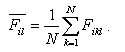 (1)
(1)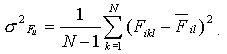 (2)
(2)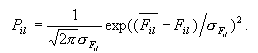 (3)
(3) 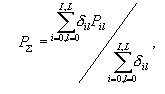 ,
(4)
,
(4)